Check a HABBY calculation
The HABBY code has a very large number of program lines written by several developers and therefore contains errors.
It is important that the user of HABBY understands the operations performed by the software, and can check them.
Here we will check the implementation of the The Instream Flow Incremental Methodology (IFIM) when using a 2D hydraulic model.
HABBY habitat calculations
The classic case consists of using a set of 3 habitat suitability curves for the variables water height, mean velocity and substrate (H,V,S) for a fish species and for a biological stage.
For a given variable, and for discrete values of the latter, the biological model provides suitability index SI given values between 0 and 1, qualifying the 'preference' of the fish, the suitability curve is thus constructed.
Equation (1) is used to calculate the habitat suitability index $\mathit{HSI_i}$ according to the user options, in a mesh of index i and area Ai of a hydraulic model, from the mean values of the variables (H,V,S) of this mesh noted $\mathit{H_i,V_i,S_i}$.
(1a) \[HSI_i=SI_H(H_i)\times SI_V(V_i)\times SI_S(S_i)\] (1b) \[HSI_i=(SI_H(H_i)\times SI_V(V_i)\times SI_S(S_i))^\frac{1}{3}\] (1c) \[HSI_i=\frac{SI_H(H_i)+ SI_V(V_i)+ SI_S(S_i)}{3}\]
In case the user decides to use only two variables for example (H,V), these equations are adapted in HABBY and become :
(1_a2) \[HSI_i=SI_H(H_i)\times SI_V(V_i)\] (1_b2) \[HSI_i=(SI_H(H_i)\times SI_V(V_i))^\frac{1}{2}\] (1_c2) \[HSI_i=\frac{SI_H(H_i)+ SI_V(V_i)}{2}\]
The logics (a) product, (b) geometric mean and © mean are respected.
In the case where the biological model is bivariate (H,V) equation (1) is written :
(1_biv) \[HSI_i=SI_{H,V}(H_i,V_i)\]
The weighted useable area WUA of the hydraulic model is obtained from equation (2) and the overall suitability index OSI from equation (3)
(2) \[WUA=\sum_{i=1}^M A_i\times HSI_i\] (3) \[OSI=\frac{WUA}{\sum_{i=1}^M A_i}\]
Note that in the particular case of a description of the substrate in percentages per $\mathit{S_k}$ classes and a calculation of habitat in % of substrate, the value of $\mathit{SI_S(S_i)}$ in equation (1) must be replaced by the formulation in equation (4). In this equation $\mathit{S_{i,k}}$ represents the % of substrate of class $\mathit{S_k}$ in mesh i, the substrate being described by a number K of particle size classes k ∈ $\mathit{[1,K]_N}$.
(4) \[{SI_{i,S}(S_{i,1},S_{i,2},..S_{i,K})}=\frac{\sum_{k=1}^K S_{i,k}\times SI_S(S_k)}{100} \]
Let us now check a HSI calculation in any mesh of a hydraulic model.
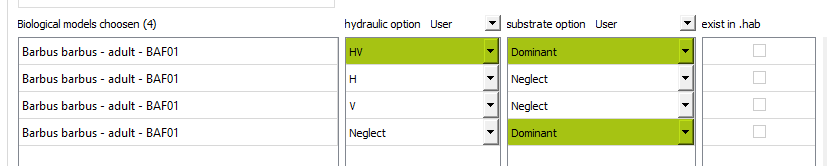
After building a .hab file with HABBY, choose a biological model for a stage, use the <hi #9BFFFF>Create duplicate from selection</hi> button to get 4 times that model. Then set the calculation options, to have not only the calculation for the 3 habitat variables, but also a calculation per variable.
Perform the habitat calculation.
To see the details of the suitability curves used, in HABBY:
- Go to the HABBY directory and open the .XML biological model with a browser (Firefox, Chrome,…) or a text editor like Notepad++.
- Identify the stage and the values defining the curves (H,V,S), for example for the water height of an adult stage:
<Stage Type=“adult”>
<PreferenceHeightOfWater>
<HeightOfWaterValues Unit="Centimeter" UnitSymbol="cm">0 5 12.5 30 60 80 300</HeightOfWaterValues>
<PreferenceValues>0 0.22 0.22 0.43 0.91 1 1</PreferenceValues>
</PreferenceHeightOfWater>
In our case, to know the suitability index of the fish for a water height of 50 cm $\mathit{SI_H}{(50 cm)}$, it will suffice to identify the values of the suitability curve framing the value sought here $\mathit{SI_H}{(30 cm)=0.43}$ and $\mathit{SI_H}{(60 cm)=0.91}$ and then to make a linear interpolation.
From the <hi #9BFFFF>Data Explorer</hi> tab after selecting your .hab file, use the <hi #9BFFFF>Data Exporter</hi> menu to export the results to GIS nodes and meshes.
Choose a mesh at random and identify the information assigned to it in the attribute table:
First check the information in the mesh:
- Substrate information S from your original data, in case your substrate is described in percentages of size classes, identify the coarser (Coarser) or dominant (Dominant) substrate that is required for the biological model.
- In the case of a 2D finite volume hydraulic simulation, identify the mean height and mean velocity, which should be those of your original data.
- In the case of a 2D hydraulic simulation in finite element, or a partly emergent mesh having been cut by HABBY, use the nodes layer and its attribute table to check them by calculating the mean values (H,V) of the 3 nodes defining the chosen mesh.
Check the $\mathit{SI_H(H)}$ , $\mathit{SI_V(V)}$ values by performing linear interpolations with the biological model data.
Check the value of $\mathit{SI_S(S)}$ directly using the correspondence with the biological model, in the case of a calculation in percentages use equation (4) for verification.
Finally check the habitat value of the $\mathit{HSI}$ mesh using equation (1).
You can also check the overall results of the hydraulic simulation from the mesh attribute table and equations (2) and (3).
Clarification:
In our case the biological model is of type “Dominant”
<PreferenceSubstrate>
<SubstrateValues ClassificationName="Code EVHA 2.0 (GINOT 1998)" Variables="Dominant">s1 s2 s3 s4 s5 s6 s7 s8</SubstrateValues>
<PreferenceValues>0.35 0.35 0.35 0.35 0.61 0.77 1 0.91</PreferenceValues>
</PreferenceSubstrate>
For some biological models the word “Dominant” can be replaced by “Coarser” or by “Percentages” depending on the construction modalities finally retained by the modellers.